Chapter 2: Foundation Models & Their Problems
Understanding the building blocks of ML and the fundamental problems that led to advanced techniques
Why Foundation Models Matter
Before diving into advanced techniques like XGBoost and Random Forests, we need to understand the foundation models they're built upon. These simple models reveal fundamental problems that drive innovation in machine learning.
The Two Pillars of ML
Most machine learning algorithms build upon two fundamental approaches:
📈 Linear Models
Core Idea: Fit a straight line (or hyperplane) through data
Examples: Linear Regression, Logistic Regression
Strength: Simple, fast, interpretable
Weakness: Can't capture complex patterns
🌳 Tree Models
Core Idea: Create decision rules by splitting data
Examples: Decision Trees, Rule-based systems
Strength: Captures complex patterns, interpretable
Weakness: Prone to overfitting
The Journey We'll Take
In this chapter, you'll discover:
- How linear models work and their bias-variance tradeoff
- Why decision trees overfit and how complexity affects performance
- Interactive demos showing these problems in action
- Why these problems led to regularization and ensemble methods
Foundation Model Selector
Choose your data characteristics to see which foundation model works best:
Recommended Model:
Linear Models: Simple but Powerful
Linear models are the foundation of machine learning. Despite their simplicity, they reveal fundamental concepts that apply to all ML algorithms.
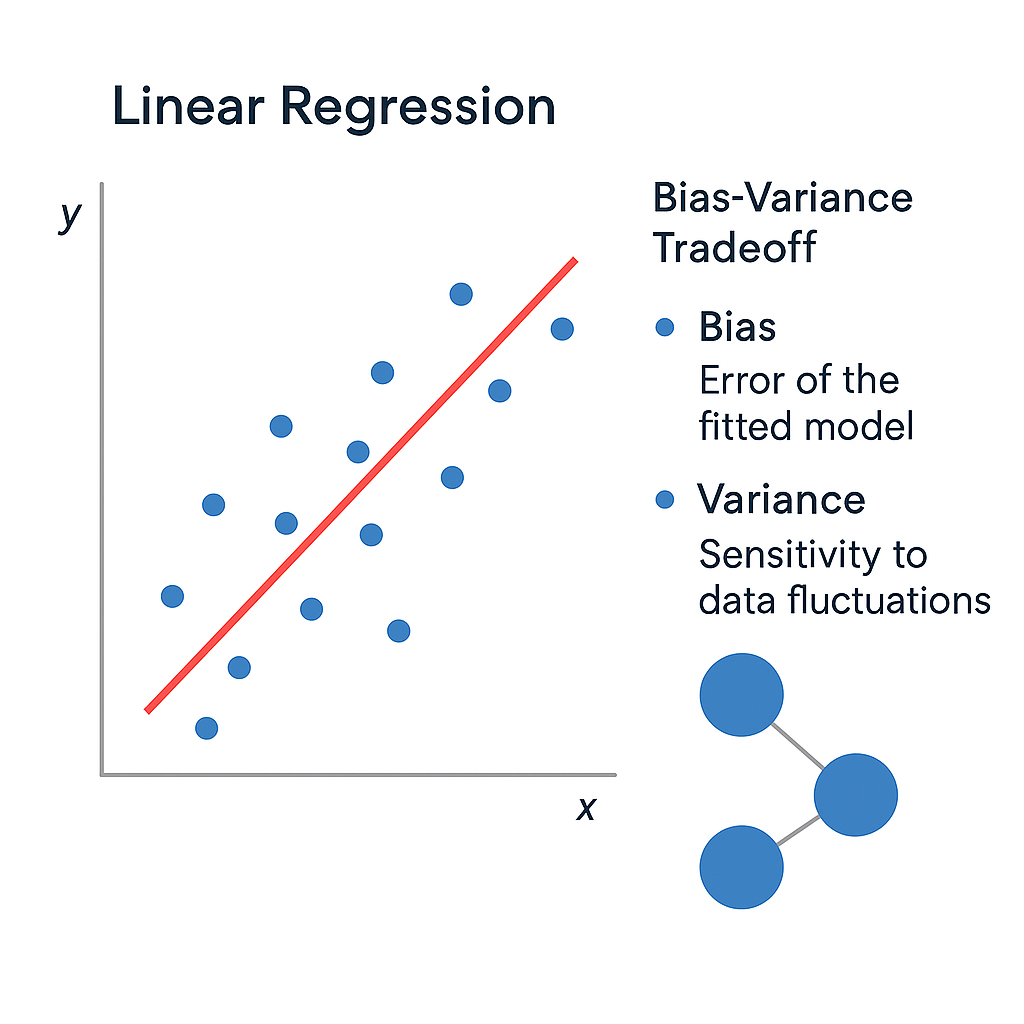
Linear Regression Demo
Interactive Parameters
The Bias-Variance Tradeoff
Linear models demonstrate the fundamental bias-variance tradeoff in machine learning:
Low Variance
- Consistent predictions across different datasets
- Not sensitive to small data changes
- Reliable and stable
High Bias (Potentially)
- May be too simple for complex patterns
- Underfitting on non-linear data
- Limited model capacity
Linear Model Limitations
As you experiment with the parameters above, you'll notice:
- Limited Flexibility: Can't capture non-linear relationships
- Feature Engineering Required: Need to manually create polynomial features
- Assumption Heavy: Assumes linear relationship between features and target
This leads us to need more flexible models... like decision trees!
Decision Trees: Flexibility with a Cost
Decision trees solve the flexibility problem of linear models but introduce their own challenges. Let's explore what makes them powerful and problematic.
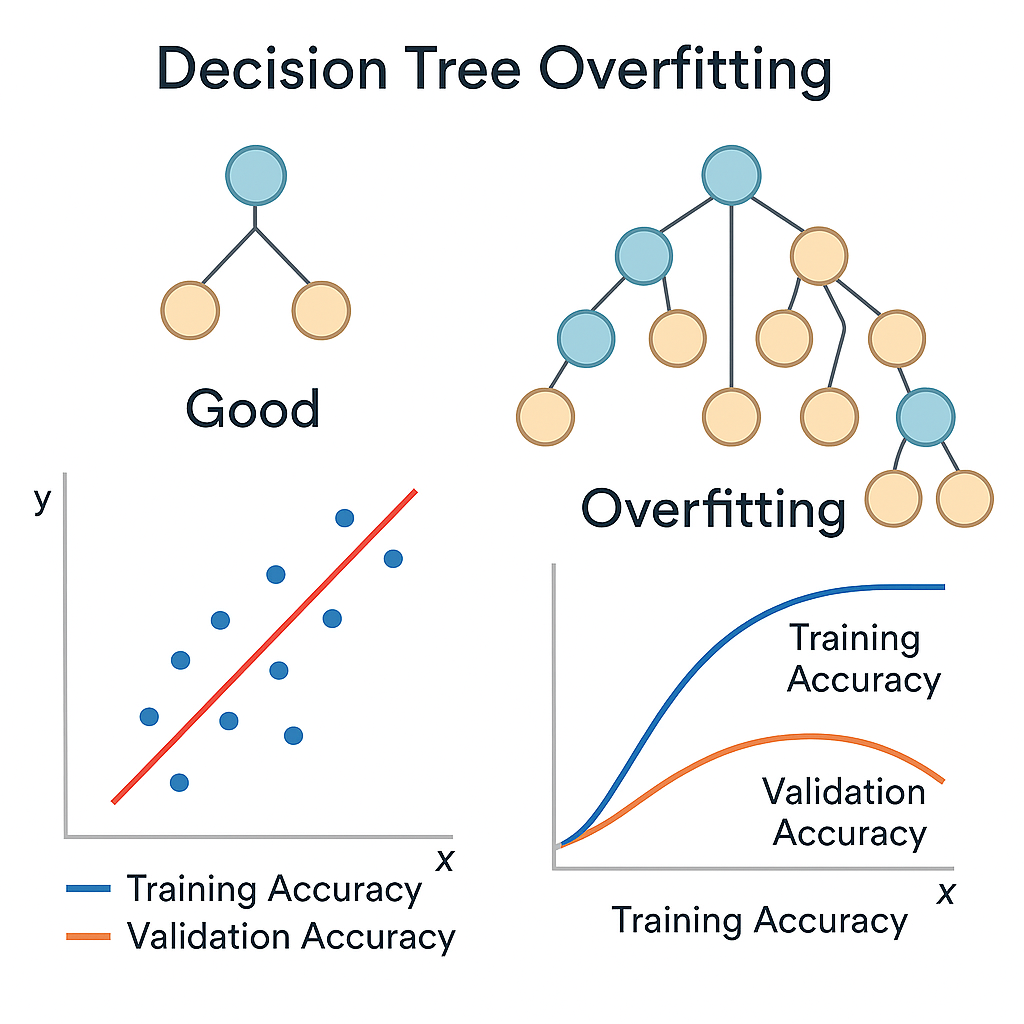
Decision Tree Overfitting
Tree Complexity Control
Interactive Overfitting Demonstration
See how decision tree complexity affects performance:
Moderate Complexity (Depth: 3)
Good balance between fitting the data and generalizing to new examples.
🎯 Decision Tree Strengths
- Non-linear Patterns: Can capture complex relationships
- Feature Interactions: Automatically finds feature combinations
- Interpretability: Easy to visualize decision paths
- No Assumptions: Works with any data distribution
- Mixed Data Types: Handles numerical and categorical features
⚠️ Decision Tree Problems
- Overfitting: Memorizes training data noise
- Instability: Small data changes create different trees
- Bias: Favors features with more split points
- Limited Expressiveness: Axis-aligned splits only
- High Variance: Very sensitive to training data
The Fundamental Problems
Now you've seen both foundation models in action. Each has critical limitations that drive the need for more sophisticated approaches.
Problem #1: The Bias-Variance Tradeoff
Linear Models
High Bias, Low Variance
- Consistent but potentially inaccurate
- Underfits complex patterns
- Limited model capacity
Decision Trees
Low Bias, High Variance
- Flexible but inconsistent
- Overfits to training data
- Unstable predictions
Solution Preview: Regularization techniques (L1/L2) and Ensemble methods balance this tradeoff!
Problem #2: Single Model Limitations
Both foundation models suffer from being "single" models:
- Limited Perspective: Each model has one way of looking at data
- Sensitive to Data: Small changes can dramatically affect results
- Error Propagation: If the model is wrong, it's completely wrong
Solution Preview: Ensemble methods combine multiple models to overcome individual limitations!
Problem Demonstration
See how the same data affects different models:
Notice how the ensemble consistently outperforms individual models!
What's Coming Next
Now that you understand the fundamental problems, you're ready to see how the ML community solved them:
- Chapter 3: Regularization techniques (L1/L2) that control overfitting
- Chapter 4-6: Ensemble methods that combine multiple models
- Chapter 7: XGBoost - the optimized implementation that wins competitions
Each solution directly addresses the problems you've discovered in this chapter!
Chapter 2 Quiz
Test your understanding of foundation models and their problems: