Chapter 3: Regularization - The Problem Solvers
Discover how L1 and L2 regularization solve overfitting problems and when to use each technique
Regularization: The Overfitting Solution
Remember the problems from Chapter 2? Linear models were too simple, decision trees were too complex. Regularization provides a mathematical way to control model complexity.
The Core Idea
Regularization adds a penalty term to the loss function that grows with model complexity:
Where λ (lambda) controls how much we penalize complexity:
- λ = 0: No penalty (original model)
- λ small: Slight penalty (minor regularization)
- λ large: Heavy penalty (strong regularization)
Interactive Regularization Concept
Adjust the regularization strength to see its effect:
No Regularization Applied
Model uses original complexity - may overfit to training data.
Two Main Types
There are two primary regularization techniques, each with different behaviors:
L1 Regularization (Lasso)
Effect: Drives some coefficients to exactly zero
Result: Automatic feature selection
Use when: You have many features and want to identify the most important ones
L2 Regularization (Ridge)
Effect: Shrinks coefficients toward zero (but never exactly zero)
Result: Smooth, stable predictions
Use when: You want to keep all features but reduce their influence
L1 vs L2: The Detailed Comparison
The difference between L1 and L2 regularization isn't just mathematical - it has profound practical implications.
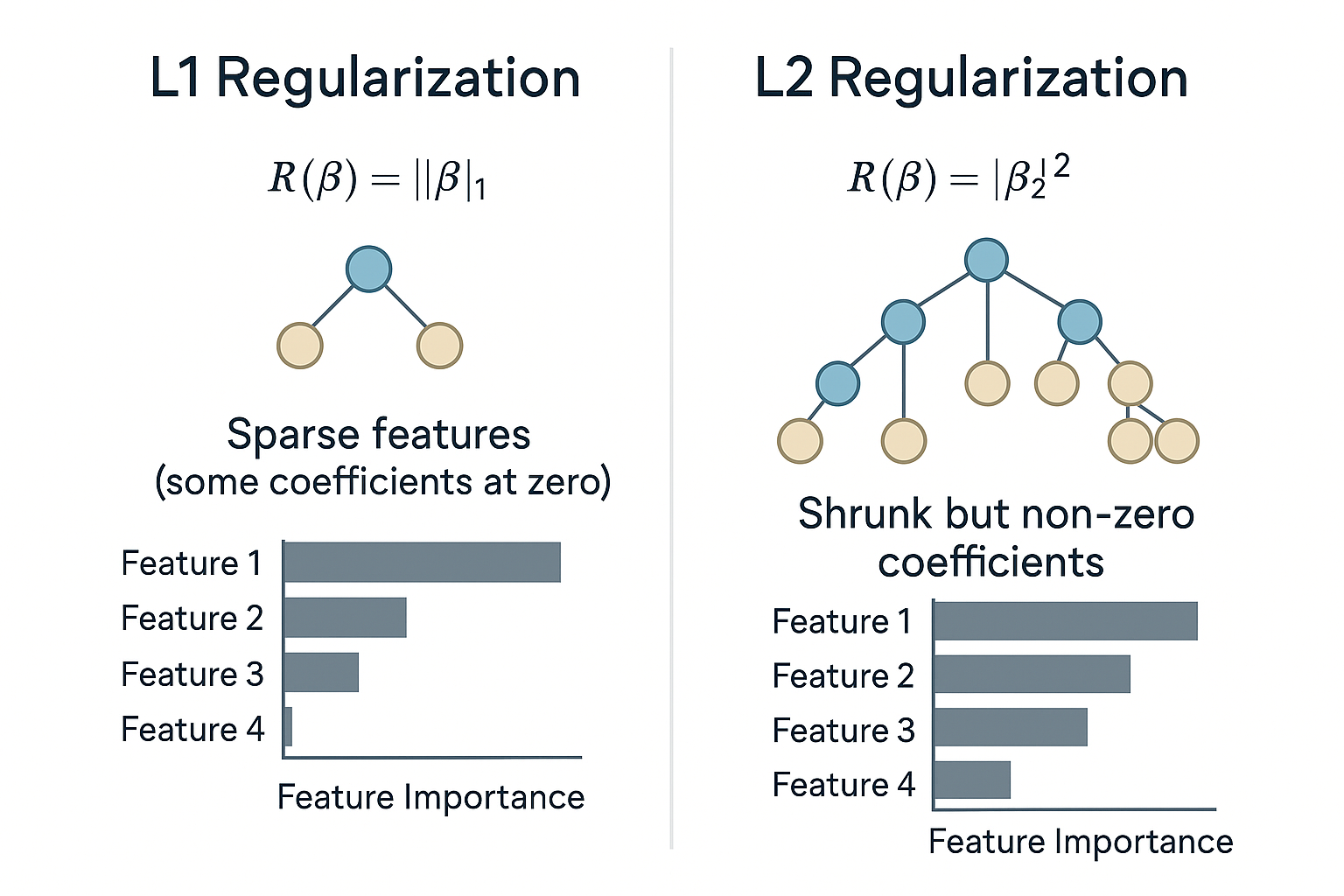
Interactive L1 vs L2 Demonstration
See how different regularization types affect feature coefficients:
L1 Regularization Active
L1 is driving smaller coefficients toward zero, effectively removing less important features.
Key Differences Explained
L1 Regularization (Lasso)
- Sparsity: Creates sparse models (many zeros)
- Feature Selection: Automatically selects features
- Interpretability: Easier to understand (fewer features)
- Instability: Can be unstable with correlated features
- Use Case: High-dimensional data with irrelevant features
L2 Regularization (Ridge)
- Shrinkage: Shrinks all coefficients uniformly
- Stability: More stable with correlated features
- Smoothness: Produces smooth, stable predictions
- No Selection: Keeps all features (with reduced weights)
- Use Case: When all features might be relevant
The Regularization Path
Understanding how coefficients change as we increase regularization strength is crucial for choosing the right λ value.
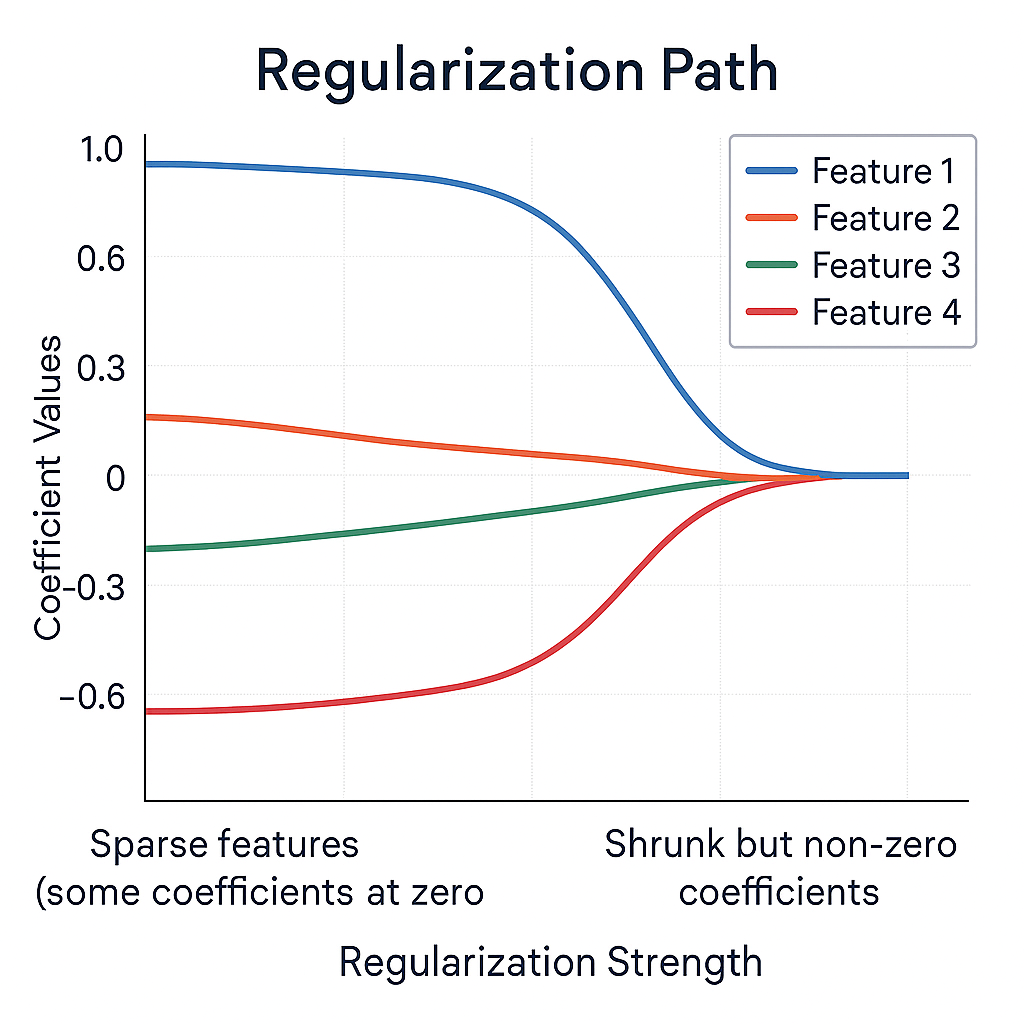
Interactive Regularization Path
Move the slider to see how coefficients evolve with regularization strength:
No Regularization (λ = 0.0)
All features retain their original importance. Risk of overfitting is highest.
Choosing the Right λ
The optimal λ balances underfitting and overfitting:
- Too Small (λ ≈ 0): No regularization, potential overfitting
- Just Right: Good balance, best validation performance
- Too Large: Over-regularization, underfitting
Cross-validation is typically used to find the optimal λ by testing different values and choosing the one that gives the best validation performance.
When to Use Each Regularization
Choosing between L1, L2, or no regularization depends on your specific situation and data characteristics.
Use L1 (Lasso) When:
- You have many features (high-dimensional data)
- You suspect only some features are truly important
- You want automatic feature selection
- Model interpretability is crucial
- You're doing exploratory analysis
Example: Gene expression data with 20,000 features but only a few are disease-related.
Use L2 (Ridge) When:
- You believe most features contribute to the outcome
- Features are highly correlated
- You want stable, smooth predictions
- You have multicollinearity issues
- Prediction accuracy is more important than interpretability
Example: House price prediction where size, location, age, etc. all matter.
Use Elastic Net When:
- You want both L1 and L2 benefits
- You have groups of correlated features
- You want some feature selection + stability
- You're unsure which regularization is better
Formula: α × L1 + (1-α) × L2
Regularization Decision Helper
Answer these questions to get a recommendation:
Make your selections above
Choose the characteristics of your data to get a personalized regularization recommendation.
Regularization Limitations
While regularization solves many problems, it has its own limitations:
- Still Single Models: Even regularized models are still just one perspective
- Hyperparameter Tuning: Finding the right λ requires cross-validation
- Linear Relationships: Doesn't help linear models capture non-linear patterns
- Feature Engineering: Still requires good feature engineering
This is why we need ensemble methods! They combine multiple models to overcome these remaining limitations.
Chapter 3 Quiz
Test your understanding of regularization techniques: